0、摘要

  本文提出了一种基于马尔可夫链和图神经网络(MEMG)的移动加密流量分类方法。我们利用马尔可夫链来挖掘流中隐藏的拓扑信息。然后在此基础上构建流图结构，在图的节点特征中加入流量的序列信息。我们还设计了一个基于图神经网络的分类器，从图中学习拓扑和顺序特征。分类器可以将图结构映射到嵌入空间中，并通过嵌入向量差对不同的图结构进行分类。

1、概念介绍

1.1 综述部分

1.1.1 基于机器学习的加密流量分类

• 依赖于统计特征：

  • 包级别的统计特征，包括接收和发送包数的平均值、最小值和最大值。

  • TLS的时间分布、未加密的报头信息和流元数据为特征

  • 流的统计特征和突发元数据（burst metadata）中的统计特征

• 依赖于流级特征（Flow-level feature）：一般方法根据流中的每个包提取流的生成概率

  • 利用加密流量的消息类型序列，构造生成概率最大的一阶马尔可夫模型对加密流量进行分类
  • 根据证书长度和首包长度，以提高二级马尔可夫模型下的流分类任务的性能
  • 利用包长度马尔可夫随机场(MRF)转换矩阵作为结构特征，构建了加密流量的指纹

1.1.2 基于深度学习的加密流量分类

• DeepPacket借助1-D CNN与堆栈自编码器，通过提取有效载荷对流量进行分类（包级）

• 有的利用注意力机制对有效载荷进行编码，最后进行分类

    缺点：没有考虑客户端到服务器之间的交互运动等其他流信息，计算开销大

1.2 文章核心观点引入

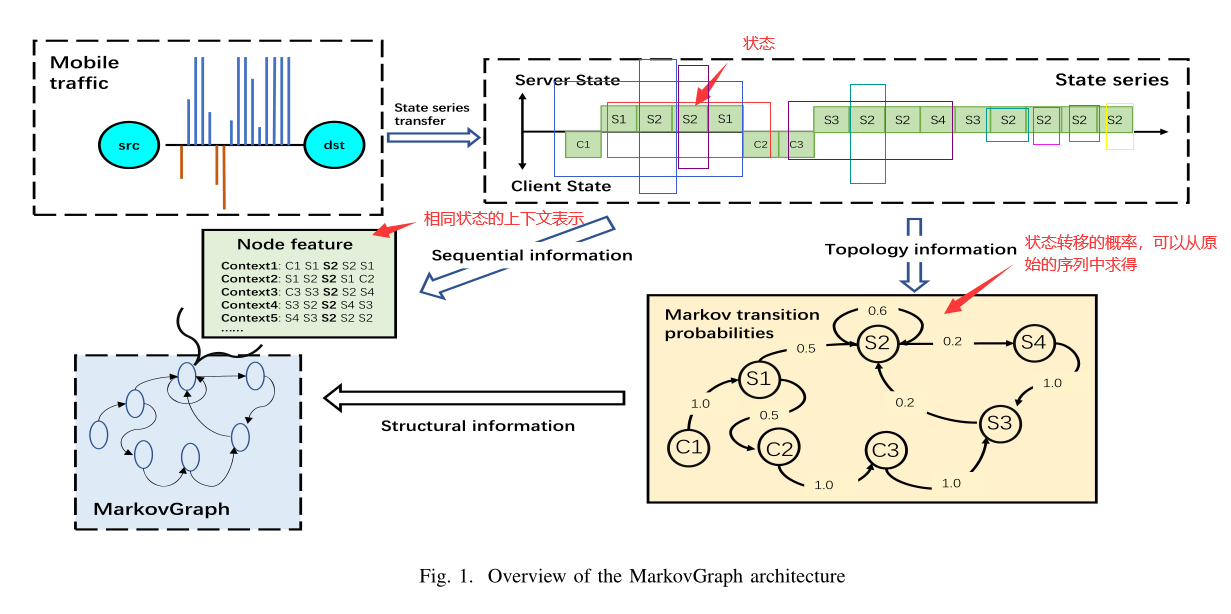
• 使用一阶马尔可夫链来构造流的拓扑结构，捕获流的隐藏拓扑信息和序列信息，称为马尔可夫图。节点为马尔可夫跃迁状态，边为跃迁概率。

• 流中每个包的上下文序列添加到图结构中作为节点特征，通过图这种数据结构，将拓扑信息与序列信息结合在一起，将流分类问题转化为图分类问题。

• GCN与MLP自动从拓扑结构信息和序列信息中提取相应特征，并将两种特征进行融合。

  • GCN提取拓扑特征

  • MLP学习序列特征

2、图构造

2.1 问题定义

  对于流序列的表示，有许多中序列表示方法表示一个流，如包长序列、消息类型序列等。这里取其中一个，假定N个样本，M个应用，对于数据集中的第i个样本x_i

$$x_i=[p_1^i,p_2^i,...,p_{li}^i]$$

li代表样本x_i的长度，x_i的每一个分值x_i^j代表时间序列为j的值

这里并没有明说这个值到底是啥，是包长？负载？

2.2 序列转换

  考虑一个五元组流的前100个数据包的长度信息，将这个100个数据包作为一个流，转为一个一阶马尔可夫链。假定MTU为1500byte，那么设定10个状态S_j,j从1-10每个状态的长度区间为150。譬如：1-150长度为状态1；…1351-1500长度为状态10。计算状态转移矩阵W，并将状态转移矩阵W按行归一化，即每一行的元素之和为1.

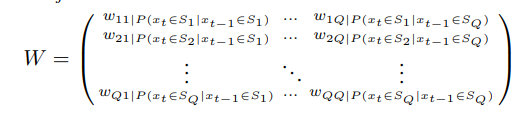
2.3 节点与节点状态

• 节点：由于根据数据包长度的大小将原始数据包长度序列转换为状态序列，所以马尔可夫图中的每个节点都包含多个数据包，其长度值属于相应的状态。

• 节点特征：由于每个节点可能包含多个数据包，故数据包的顺序信息可能会难以提取，故对数据包状态序列进行切片操作：

  • 每个数据包的上下文是状态序列的前2个数据包和后2个数据包，作为该数据包状态的顺序信息
  • 对于处于相同状态的所有包，使用RNN对那些包的上下文进行压缩，最后形成p维向量，p取128，作为节点特征

  2.4 马尔科夫图的构造

  这里给出了前面所有步骤的算法描述:

• 输入：流序列、状态空间、窗口大小
• 输出：马尔科夫图

• 具体描述：
  • 1-3行的循环：将原始流序列X_i转为状态序列B_i（4），对S取模，这里S=150
  • 5-7行的循环：通过得到的状态序列B_i构造马尔科夫图的节点集合
  • 8：计算状态转移概率矩阵M
  • 9-15：将M的值作为权重赋给马尔科夫图的边
  • 16：初始化状态特征集合F_i
  • 17-19：对窗口w内的上下文状态序列，进行切片，作为状态序列的顺序信息添加到F_i中
  • 20-22：对F特征集合的对每一个特征，利用RNN压缩映射到128维向量，作为节点的特征向量
  • 23：得到最终的马尔科夫图G

2.5 马尔科夫图MG的优势

  这里作者任务MG至少包含流量的两种特征：

• 马尔科夫链能包含流量的拓扑信息

• 包长度序列也能在拓扑信息中表示

  

  3、图神经网络结构

  原始流量转为图结构后，使用GCN与MLP进行特征抽取进行分类。

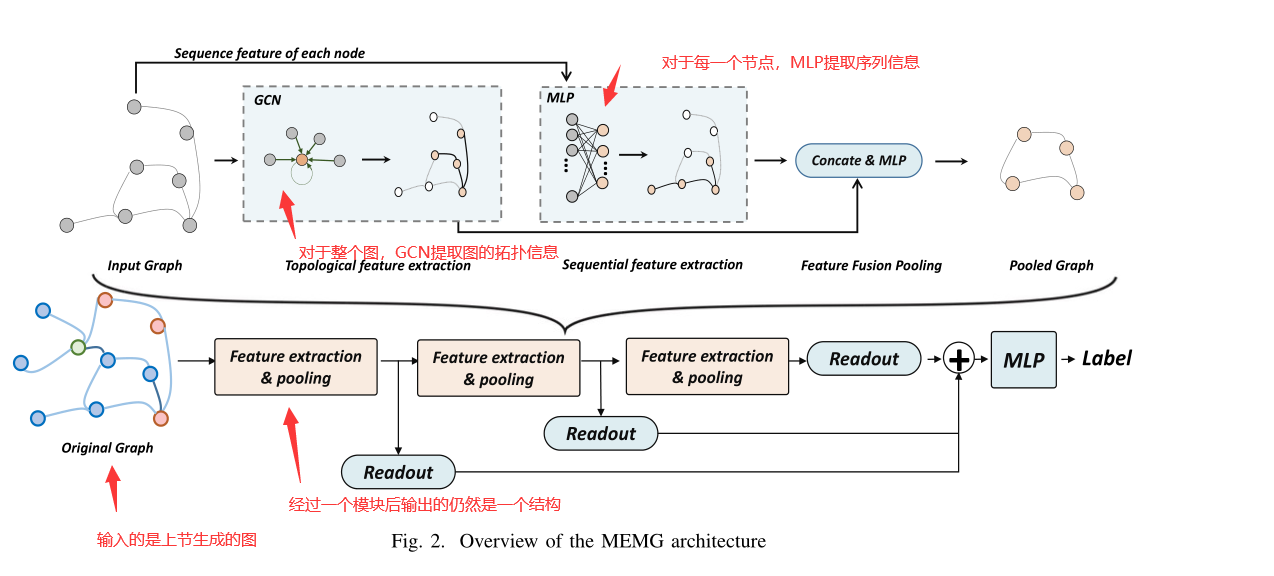
  对于图中橙色模块的，分为特征提取与特征池化

• 特征提取：

  • 提取图的全局拓扑信息：使用GCN，每次使用当前节点的邻接节点进行节点状态更新，得到F₁
  • 提取每一个节点状态的顺序信息：使用MLP，得到F₂

• 特征池化：减少参数，获得更鲁棒的泛化，缓解过拟合

  $$F_{fusion}=Activate(MLP([F_1;F_2]))$$

  [;]表示拼接，根据对应的分数对节点进行排序，取前k个节点的特征，论文中k取5

为了考虑到模型结构的全局与局部特征，对每个橙色结构块的输出进行拼接考虑，作为最终分类器的输入（图中的Readout模块）

• 分类器模块：MLP结构，采用交叉熵损失。

4、实验

• 与机器学习方法与其他的马尔科夫族方法做了对比

• 似乎没有做消融实验，不能证明模型每个结构的必要性

• 实验证明在精度性能的优越性下，MEMG保证的小的内存开销与快速收敛

• 似乎也没有跟目前的主流的深度学习方法做对比

5、总结与思考

  马尔科夫图+GNN可以凑一起，并且理由解释得很好，什么拓扑信息、顺序序列信息怎么怎么提取。